Introduction to Lewis signaling games with Python

What does it mean for a message to mean? In this blog post, I provide an accessible introduction to one formal framework developed for addressing this question: Lewis signaling games. A Lewis signaling game demands a sender and a receiver to invent a communication protocol so that the receiver can act based on information only available to the sender and maximize reward for both of them. A non-trivial semantics (a formal theory of meaning) can be formulated in terms of Lewis signaling games and the whole signaling games framework is well-suited to tackle research problems in cognitive science and artificial intelligence (among others).

A toy Lewis signaling game

More formally, a Lewis signaling game consists of

• a world (a set of states),
• a sender (a mapping from a world state to a message),
• a receiver (a mapping from a message to an action), and
• a reward function assigning each (world state, action) pair a scalar reward.

We are specifically interested in cases when the optimal action depends on the state of the world available only for the sender. In such a case, the sender is incentivized to transmit the information about the state to help the receiver make an informed decision.

The world and the reward function

Let us illustrate the concept of a Lewis signaling game with a toy Python implementation.

class World:
    def __init__(self, n_states: int, seed: int = 1701):
        self.n_states = n_states
        self.state = 0
        self.rng = np.random.RandomState(seed)
        
    def emit_state(self) -> int:
        self.state = self.rng.randint(self.n_states)
        return self.state
    
    def evaluate_action(self, action: int) -> int:
        return 1 if action == self.state else -1

World is a thin wrapper over a random number generator. At each time-step of the simulation, our world is in one out of a number of unordered, distinguishable states. We label possible states with integers from 0 to n_states.

World also defines a reward function under the evaluate_action method. Our toy example is what is usually called a reference game: each action of the receiver corresponds to a world state and the sender must make the receiver acts accordingly to the world state only sender observes. The reward is 1 is action number equals world state number and -1 otherwise.

The agents

The sender implements a stochastic policy: at each round of the game, it samples a message to send from a conditional categorical distribution \(p(\text{message}\vert\text{world_state})\) parametrized by a n_inputs ✕ n_messages matrix of unnormalized weights for each (world_state, message) pair. Intuitively, the larger the weight for a (world_state, message) pair, the more probable it is for the sender to send a message upon observing a world_state.

The weights matrix is initialize with zeros to encode a uniform distribution. The weights are subsequently reinforced based on rewards the sender gets for sending a message upon observing a world_state: increased by positive rewards and decreased by negative. The probability of choosing a message is thus proportional to the total accumulated rewards from choosing it in the past. This simple algorithm is known as Roth–Erev model in psychology and economics. Engineers and computer scientists would probably prefer to call it online Monte Carlo policy improvement.

class Sender:
        
    def __init__(self, n_inputs: int, n_messages: int, eps: float = 1e-6):
        self.n_messages = n_messages
        self.message_weights = np.zeros((n_inputs, n_messages))
        self.message_weights.fill(eps)
        self.last_situation = (0, 0)
        
    def send_message(self, input: int) -> int:
        probs = np.exp(self.message_weights[input, :])/np.sum(np.exp(self.message_weights[input, :]))
        message = np.random.choice(self.n_messages, p=probs)
        self.last_situation = (input, message)
        return message

    def learn_from_feedback(self, reward: int) -> None:
        self.message_weights[self.last_situation] += reward

The code is analogous for the receiver, with the exception that the receiver chooses actions based on the messages and its weights matrix encodes the unnormalized distribution \(p(\text{action}\vert\text{message})\).

class Receiver:
        
    def __init__(self, n_messages: int, n_actions: int, eps: float = 1e-6):
        self.n_actions = n_actions
        self.action_weights = np.ndarray((n_messages, n_actions))
        self.action_weights.fill(eps)
        self.last_situation = (0, 0)
        
    def act(self, message: int) -> int:
        probs = np.exp(self.action_weights[message, :])/np.sum(np.exp(self.action_weights[message, :]))
        action = np.random.choice(self.n_actions, p=probs)
        self.last_situation = (message, action)
        return action

    def learn_from_feedback(self, reward: int) -> None:
        self.action_weights[self.last_situation] += reward

Learning dynamics

For our toy experiments, I assume n_inputs = n_messages = n_actions = 10. Sender and receiver are jointly optimized based on the success of the receiver. The learning should converge after about a thousand rounds of the game.

sender, receiver = Sender(10, 10), Receiver(10, 10)
world = World(10)
for _ in range(2000):
    world_state = world.emit_state()
    message = sender.send_message(world_state)
    action = receiver.act(message)
    reward = world.evaluate_action(action)
    receiver.learn_from_feedback(reward)
    sender.learn_from_feedback(reward)

Below I plot the weight matrices for the sender and the receiver as they evolve through training. As expected, for each state/message the probability mass concentrates over a single message/action. In other words, the each weight matrix converges to a permutation matrix. Additionally, because our reward function defines a reference, the sender’s final matrix is an inverse (or, for that matter, a transpose) of the receiver’s final matrix.

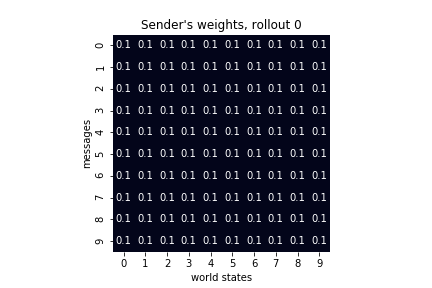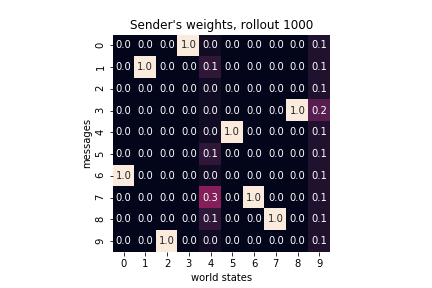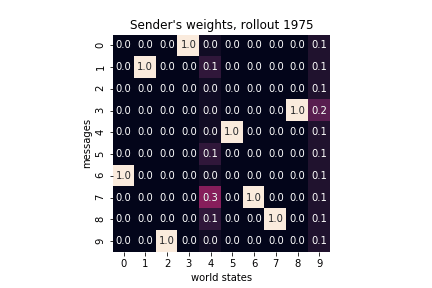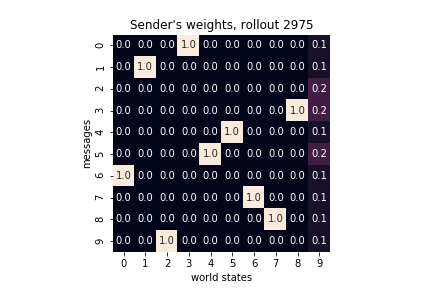How meaning emerges

Sender’s and receiver’s weights matrices jointly define a communication protocol. From a game-theoretic point of view, it is a Nash equilibrium: both the sender and the receiver would be worse off deviating from the protocol. But what justifies the particular choice of a communication protocol? Both weight matrices initially encoded uniform probability distributions and, given the constrains of our game, there are \(10!\) possible communication protocols (or, permutations of each weight matrix). To which will the sender-receiver dynamics converge depends purely on the random seed of the World. To put it differently, it is a matter of convention and can social conventions emerge via symmetry breaking in agents’ weights matrices.

It is through symmetry breaking that meaning arises out of nothing. Meaning of a message in a signaling game can be defined in terms of how it affects \(p(\text{message}\vert\text{world_state})\) and \(p(\text{action}\vert\text{message})\). The change in the first distribution gives rise to descriptive content of a message while the change in the second distribution gives rise to imperative content. Let us focus the remaining discussion on imperative content. The information conveyed by a message to the receiver is simply the point-wise mutual information between the message and the action, i.e. \(\text{log}(\frac{p(\text{action}\vert\text{message})}{p(\text{action})})\). The information content of a message is a vector of point-wise mutual informations between the message and each of the actions available for the receiver. That is, for a game with \(n\) available actions for the receiver (\(a_1, a_2, \ldots, a_n\)) the imperative meaning of message \(m\) is

Such a vector of log probability ratios is known as an s-vector. Intuitively, imperative content of messages describes how acquiring the message affects the behavior of the receiver. In our toy example, the prior \(p(\text{action})\) is uniform, but in general the receiver may have a default course of action subject to change depending on a message (think of a busy meerkat suddenly hearing a “predator approaching” alarm call). Another feature of our toy example is that training converges to a communication protocol consisting of a one-to-one mapping between messages and actions, which entails that each message move all the probability mass of \(p(\text{action}\vert\text{message})\) over a single action. The meanings of our messages are vectors consisting of negative infinities for all actions except the correct one \(a_c\):

The s-vector semantics

How seamlessly Lewis signaling games integrate with information theory is indeed a major strength of the framework. Note, however, that information content (a vector of log probability ratios) is a richer object than the quantity of information conveyed in a message (a scalar). How the message changes the distributions is more than just how much it changes the distribution. Imperative information content has a normative aspect as it describes the behavior expected of the receiver upon receiving the message. In formal semantics parlance, the s-vector gives rise to satisfaction conditions. The receiver may either respect the satisfaction conditions of a message or fail to do so (in case when the empirical distribution over its actions does not converge to the posterior \(p(\text{action}\vert\text{message})\)).

More formally, a semantics for a given communication protocol assigns a unique, evaluable formal object to each message such that it uniquely characterizes the content of that message, e.g. determines in what circumstances the message is to be sent (descriptive content) or what should be done upon receiving it (imperative content). The unique, evaluable formal objects called meanings are traditionally taken to be sets of possible worlds or situations. The idea that the s-vector is a good candidate for a meaning was first proposed by Skyrms and has recently been defended by Isaac (2019) under the name of s-vector semantics. This approach is theoretically interesting because it has very few theoretical commitments: it only assumes the axioms of probability and the existence of a sender and a receiver. It also explicitly ties the meaning of a message to its use and how the meaning evolves, as well as to (Bayesian) inference involved in meaning comprehension and informed action. From a computational point of view, taking the set of available meanings to be a vector space is very in line with distributional approaches to semantics that underlie contemporary natural language processing.

One curious property of the s-vector semantics is that it is not recursively defined. Consider an extension of the toy signaling game described above when we allow for complex messages composed of primitive messages, e.g. \(m = m_1 \circ m_2\). In a traditional, recursive semantics the meaning of \(m\) would be a function of the meanings of \(m_1\) and of \(m_2\). Note, however, that the one cannot infer the joint distribution \(p(m_1, m_2)\) from marginal distributions \(p(m_1)\) and \(p(m_2)\). How compositional meaning can arise and be represented in distributional terms is an active area of research in both computational linguistics and cognitive science.

Further reading

The study of signaling games was pioneered by David Lewis, who analyzed the emergence of social conventions in game-theoretic terms his seminal Convention: A Philosophical Study. While Lewis’ motivation was philosophical (explicating the notion of truth by convention), signaling games are extensively used in economics (e.g. to model labor market or stock exchange) and biology (e.g. to model sexual selection and animal communication).

Brian Skyrms’ Signals is definitely the most comprehensive and entertaining read on the subject. The book describes how a number of very non-trivial behaviors (e.g. deception, logical inference, teamwork) can arise in signaling games with reinforcement learning or evolution (replicator dynamics). Barrett and Skyrms (2017) recently explored generalized signaling games: games evolved out of simpler games through recursive nesting (modular composition) or iterative adaptation (template transfer).

Signaling games were widely studied in cognitive science and artificial intelligence, albeit not always called by their name. Milestones include Cangelosi, 2001 and Steels & Belpaeme, 2005. The study of the emergence of communication has recently gained momentum in the machine learning community, partly due to a series of workshops at NeurIPS conference. Recent advances focus on modeling complex linguistic phenomena (like compositional communication) by using more powerful agents (e.g. implemented as deep neural networks) and more efficient training procedures. EGG is probably the best library to get started with writing code for your own experiments.

A Jupyter notebook accompanying this blog post is available on GitHub.